Bit-Flipping Attacks against Cipher Block Chaining Algorithms
When you consider attacks against cryptographic ciphers, you usually think of those attacks against the cipher itself, which allow you to break the code and recover the plaintext. It’s important to remember that the message can be attacked, even when the cipher remains unbroken and, indeed, even the full message is unknown. Consider a quick example with a plain stream cipher.
Instead of XOR bits, use decimal digits and modular arithmetic. Note that XOR is the exclusive-or operation. It simply compares two inputs and returns true if they are different. Of course, with binary, the inputs are either true (1) or false (0), so if the inputs are both 1 or both 0, the result will be 0.
Make your message MEET AT NOON using 01 for A, 02 for B, and so on, and your key 48562879825463728830:
13050520012014151514 + 48562879825463728830 -------------------- 51512399837477879344
Now, suppose you can’t crack the algorithm, but you can intercept the encrypted message in transit and flip some digits around. Using that same key, throwing in some random numbers would just result in nonsense when you decrypt. But change a few of the final digits—now your key is 51512399837469870948 and suddenly the plaintext becomes MEET AT FOUR.
You didn’t attack the algorithm; you attacked the message and caused someone some trouble. Now, this is a very rough example designed to illustrate the concept of attacking messages. Now that you’ve had some fun with modular arithmetic, dive into the more complex stuff.
Block ciphers and modes of operation
In a stream cipher, data is encrypted one bit at a time until it’s done. This is in contrast to a block cipher, which, as the name suggests, encrypts data in fixed-length blocks. From a security standpoint, this concept implies that a secure encryption is easily achieved for a single block of data. You could have high-entropy key material with the same length as the block. But your plaintext is never that short; the data is split up into multiple blocks. How you repeatedly encrypt block after block and link everything together is called a mode of operation. As you can imagine, the design of a block cipher’s mode of operation is where security is made and broken.
Now, look at probably the simplest (medieval) block cipher mode of operation called Electronic Codebook (ECB) mode. It is named so because it’s inspired by the good old-fashioned literal codebook of wartime encryption efforts: you encrypt and decrypt blocks of text without using any of that information to influence other blocks.
This would probably work just fine if you were encrypting random data, but who’s doing that? No one; human-composed messages have patterns in them. Now, here’s a demonstration with openssl and xxd on Kali, which is a nice way to encrypt something and look at the actual result.
Tell the world that you’re an elite hacker and repeat the message over and over again—for emphasis. Encrypt it with AES-128 operating in ECB mode and then dump the result with xxd:
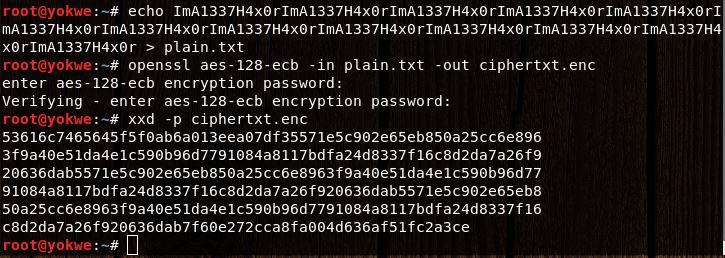
At first glance, you’ll see just a bunch of random-looking hexadecimal characters jumbled together. A solid encrypted message should be indistinguishable from random data, so your work here is done. But, hark! Upon closer inspection, a very long string of characters repeats throughout:
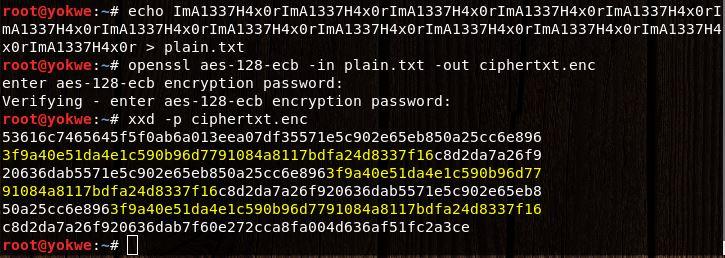
You might look at this and think, so what? You still don’t know what the message is. In the realm of cryptanalysis, this is a major breakthrough. A simple rule of thumb about good encryption is: the ciphertext should have no relationship whatsoever with the plaintext. In this case, you already know something is repeating. The effort to attack the message is already underway.
Introducing block chaining
With ECB, you were at the mercy of your plaintext because each block has its own thing going on. Enter Cipher Block Chaining (CBC), where you encrypt a block just like before—except before you encrypt the next block, you XOR the plaintext of the next block with the encrypted output of the previous block, creating a logical chain of blocks.
The hacker in you must be thinking now: if you XOR the plaintext block with the encrypted output of the previous block, what’s the XOR input for the first block? Nothing gets past you. Yes, you need an initial value, appropriately called the initialization vector (IV):
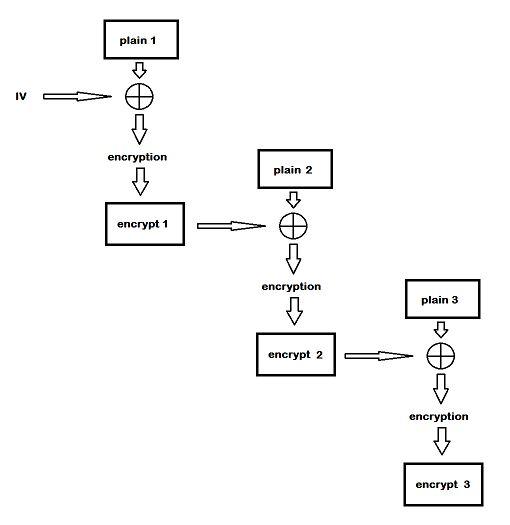
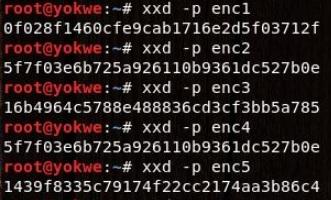
With CBC, security is highly reliant on the IV. Before moving on, here’s one more openssl demonstration with CBC, but repeat the IV. Using xxd, you’ll see if you can find a pattern in the plaintext blocks:
Setting up your bit-flipping lab
Now attack a web application to pull off the bit-flipping attack. What’s nice about this hands-on demonstration is that you’ll be left with a really powerful web app hacking lab for your continued study. Use the OWASP project Mutillidae II. Host Mutillidae II on the XAMPP server stack, as the initial setup is fast and easy, and it’s a powerful combination. However, if you’re comfortable loading it into whatever web server solution you have, go for it.
If you’re following this lab, then first download the XAMPP installer, chmod it to make it executable and then run the installer:
![]()
Once this is installed, you can find /opt/lampp on your system. Download the Mutillidae II project ZIP and unzip everything into /opt/lampp/htdocs—that’s it. Run ./lampp start and then visit your IP address in a browser:
Manipulating the IV to generate predictable results
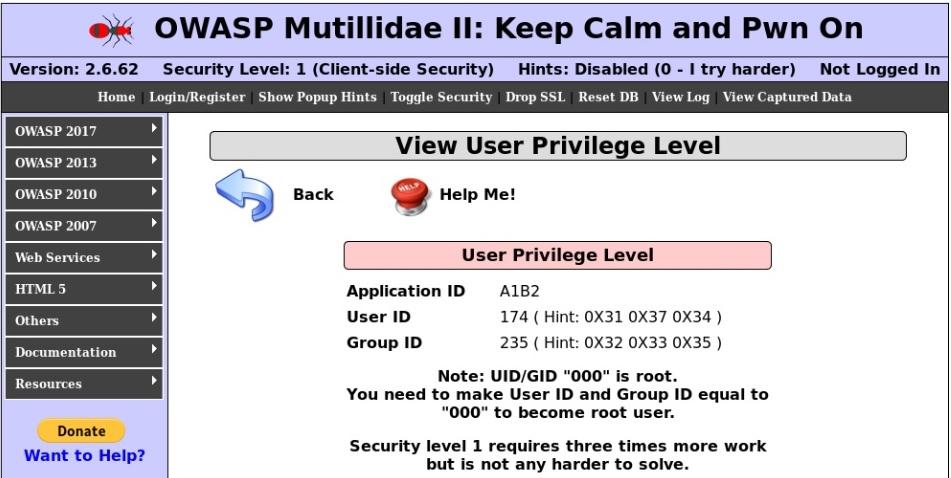
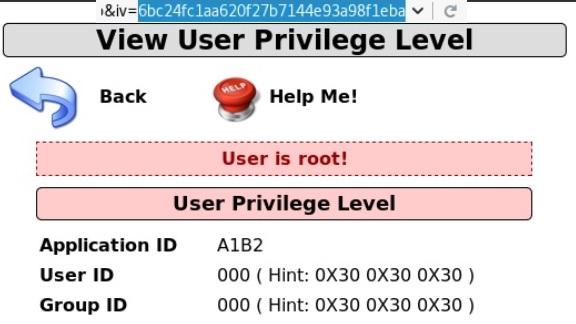
Navigate to OWASP 2017 on the left, then Injection | Other and CBC Bit Flipping to arrive at the site shown in the above screenshot. Here you’re currently running with User ID174 with Group ID235. You need to be user 000 in group 000 to become the almighty root user. The site is protected with SSL, so intercepting the traffic in transit would be a bit of a pain. What else do you notice about this site?
How about the URL itself? https://192.168.108.104/index.php?page=view-user-privilege-level.php&iv=6bc24fc1ab650b25b4114e93a98f1eba
It’s an IV field, right there for the taking. You’ve seen how the IV is XOR with the plaintext before encryption to create the encrypted block. So, manipulating the IV would necessarily change the encrypted output. First, take a look at the IV itself, 6bc24fc1ab650b25b4114e93a98f1eba. You know that it’s hexadecimal and it is 32 characters long; thus the length is 128 bits.
Now, modify the IV in the URL, submit it, and see if anything happens. Change the initial character into a zero, making the IV 0bc24fc1ab650b25b4114e93a98f1eba:
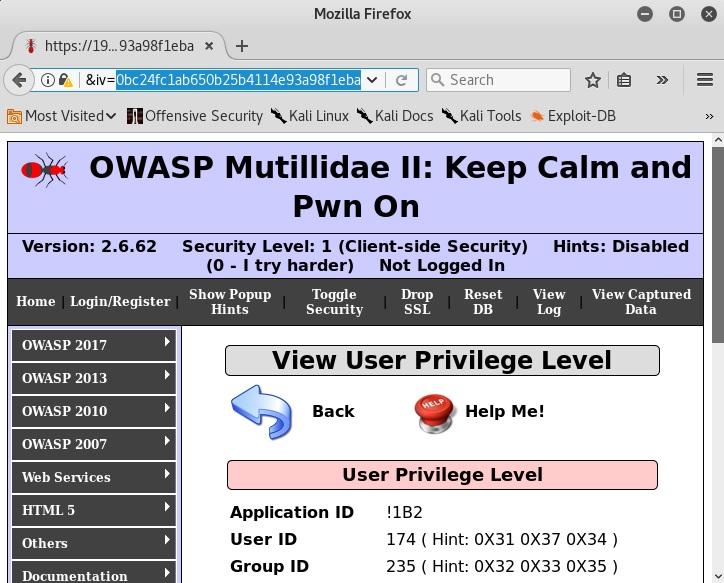
Your IDs didn’t change, but check out what happened to the Application ID. Now it’s !1B2. It used to be A1B2. What if you change the first two hexadecimal digits to zeroes? Your Application ID is now *1B2.
If you change the first three, then the next character in the Application ID falls apart because the resulting binary doesn’t have an ASCII representation. Now you know that the first two hexadecimal characters in the IV (8 bits) modify the first ASCII character in the Application ID (8 bits). This is a breakthrough that pretty much translates into the final stretch to privilege escalation.
You’ve just established a direct relationship between the plaintext and the IV, which means that you can figure out the ciphertext. And when you know two of the three, in any order, you can calculate the third by virtue of simple binary XOR math. Now, you haven’t found where the hexadecimal digits are. The User ID and Group ID can be manipulated just yet, but see if you can figure out this relationship based on what you have so far.
You saw the Application ID change from A to ! to *. Thus, the ID is represented in ASCII, the most common modern standard for character encoding. What’s important here is that a single ASCII character is 8 bits (1 byte) long.
Hexadecimal, on the other hand, is simply a base-16 numeral system. You see hexadecimal everywhere in the gritty underbelly of computing because 16 is a power of 2, which means converting from base-2 (that is, binary) to base-16 is easy. 2 to the power of 4 equals 16, which means a hexadecimal digit is 4 bits long. Back to the lab:
| IV hexadecimal digits | Binary representation | Application ID result in binary (ASCII) |
| 6b | 0110 1011 | 0100 0001 (A) |
| 00 | 0000 0000 | 0010 1010 (*) |
Do you see your golden ticket yet? Well, XOR the binary IV values with the known binary ASCII result in the Application ID, because if they match, then you have the value that was XORed with the IV values to generate the Application ID. Remember, if you know two out of three, you know the third.
First, the original IV:
- Hexadecimal6b: 0110 1011
- ASCIIA: 0100 0001
- XOR result: 0010 1010
And now, your test manipulated IV:
- Hexadecimal00: 0000 0000
- ASCII*: 0010 1010
- XOR result: 0010 1010
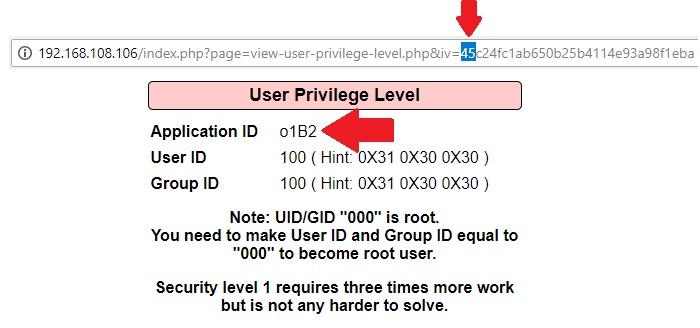
This is why they call it bit-flipping. You figured out that the application is taking this byte of the IV and XORing it with 0010 1010 during decryption. Test your theory by calculating what you’ll get if you replace the first two hexadecimal digits with, say, 45:
- Hexadecimal45: 0100 0101
- Ciphertext XOR: 0010 1010
- Binary result: 0110 1111
01101111 encodes to an ASCII o (lowercase O). Test your theory and see if you end up with an Application ID of o1B2:
This is an exciting breakthrough, but you just picked up on some behind-the-scenes mechanisms; it still isn’t the root. So, get to work on finding the bits you really need to flip.
Flipping to root – privilege escalation via CBC bit-flipping
You probably thought that you could just step through hex pair by hex pair until you find the right spot and flip your way to victory. Not exactly!
The way User ID and Group ID are encoded is a little funky, and there’s a different piece of ciphertext being XORed against when you work your way down the IV. At this point, it’s pure trial and error while relying on the hints you’ve already gathered. Here are some notes:

It’s a little tedious, but you only need to play with a few characters to understand what’s going on here:
- Though each position is 8 bits, only modifying the final 4 bits would change the User ID/Group IDvalue in that position. For example, note that when you replaced the two hexadecimal characters in a position with 00, the result breaks (that is, the resulting binary value isn’t ASCII-friendly).
- Do the XOR calculation on the trailing 4 bits of each byte to find the key that you need and discover that the value isn’t the same for all positions.
The hacker in you was already expecting unique XOR values for each character, right? The stream of bits that are being XORed with the IV wouldn’t really be a byte-long repeating pattern. The effort to discover these values pays off, though, because all you have to do now is calculate the XOR for each position.
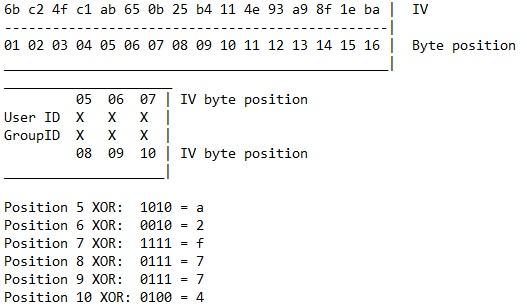
XOR the hexadecimal character in the IV with the hexadecimal of the User ID/Group ID in that position, and the result is the enciphered bits at that position. And since you’re looking for all zeroes, the result for each position is the binary equivalent of the hexadecimal character you need to put in the IV instead of the original.
Now, translate this conclusion with an example from the IV: position 09 is b4, which corresponds to the middle digit in the Group ID, which is 3. Hexadecimal 4 in binary is 0100 and hexadecimal 3 is 0011. 0100 XOR 0011 equals 0111. 0111 is the binary equivalent of 7, which means you would replace b4 with b7 to get a 0.
Now, repeat this calculation for all six positions. The byte-long IV positions 05 through 10 correspond to the User ID and Group ID. The final 4 bits of each position needs to be replaced with the hexadecimal values (in order) a2f774 to get the root. Position 05 in the original IV was ab, so it becomes aa; position 06 was 65, so it becomes 62; and so on.
Thus, the IV from the 5th byte to the 10th byte changes from ab650b25b411 to aa620f27b714:
The moment of truth: Change the IV from 6bc24fc1ab650b25b4114e93a98f1eba to 6bc24fc1aa620f27b7144e93a98f1eba:
If you found this article interesting, you can explore Phil Bramwell’s Hands-On Penetration Testing on Windows to master the art of identifying vulnerabilities within the Windows OS and develop the desired solutions for it using Kali Linux. Hands-On Penetration Testing on Windows will teach you advanced techniques to attack Windows environments using coding principles that allow you to leverage powerful Python scripts and shellcode.




